
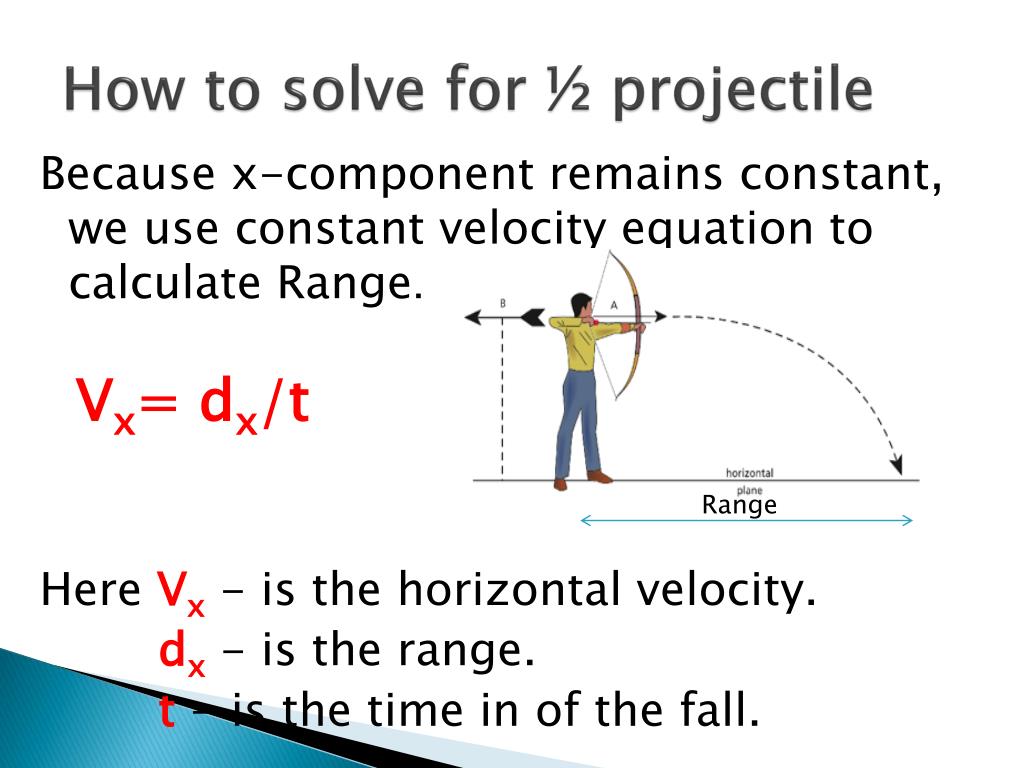
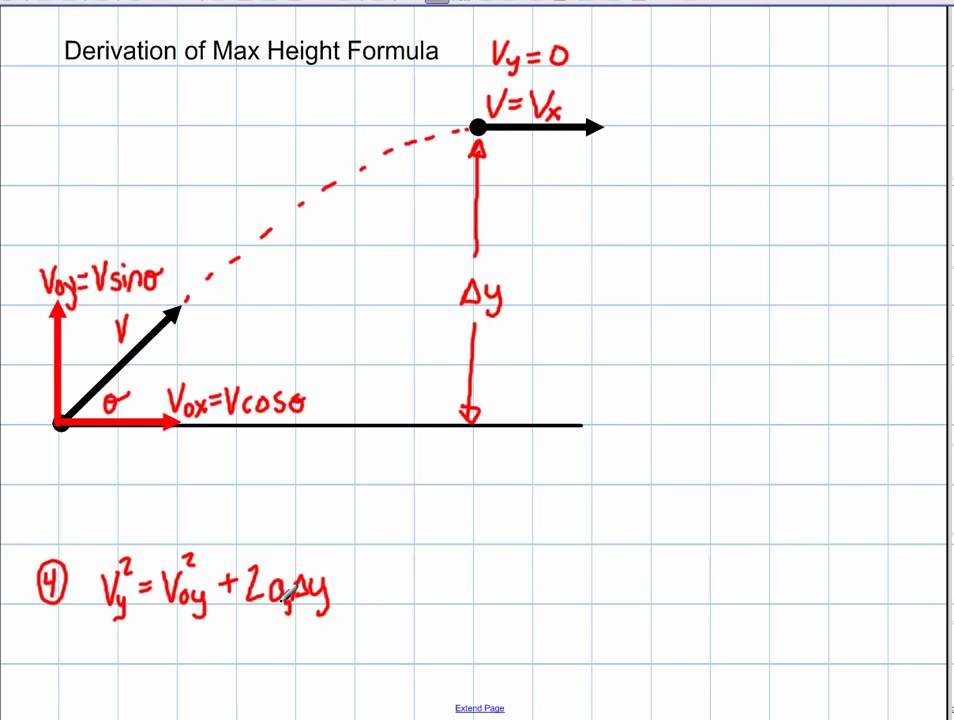
Initial horizontal velocity remains constant and does not change. Its magnitude decreases when a object travels upwards and increases when it travels downwards. Initial vertical velocity changes throughout projectile motion. Find its initial horizontal and vertical velocities.Ĭonstruct a right-angled triangle from vectors: Situations in which this type of initial velocity occurs will be explored and clarified in practice questions later.Ī projectile is launched at 60 ms -1 at an elevation of 30 0. The initial velocity can be negative because the initial direction of a projectile can also be downwards as shown below. Since the triangle is right-angled, the three vectors’ relationship can also be summarised by Pythagoras’s theorem. The relationship between initial vertical and horizontal velocity is described by:. Using trigonometry, initial horizontal and initial vertical velocities can be expressed in terms of the initial velocity. The relationship between initial velocity, initial horizontal and vertical velocity can always be represented by the right-angled triangle with q (as shown in the diagram) is the angle at which the projectile leaves the horizontal plane (usually the ground). Initial horizontal velocity is typically written as u x– subscript x is used to represent the horizontal rectilinear motion. Initial vertical velocity is typically written as u y– subscript y is used to represent the vertical rectilinear motion. Initial velocity is typically written as u. This is done by constructing a right-angled triangle from vectors. The initial velocity can always analysed as and resolved into two components: horizontal and vertical velocities. All objects at the beginning of their projectile motion must possess a non-zero initial velocity. Solve problems, create models and make quantitative predictions by applying the equations of motion relationships for uniformly accelerated and constant rectilinear motion. Apply the modelling of projectile motion to quantitatively derive the relationships between the following variables:. Understanding these calculations can help us to predict the trajectory of projectiles and make more accurate predictions in fields such as ballistics and engineering. The equations of motion allow us to calculate key aspects of projectile motion such as range of flight, flight time, and maximum height. In conclusion, projectile motion is the motion of an object projected into the air and subject only to the force of gravity. Where h is the maximum height, V₀ is the initial velocity, alpha is the angle of projection and g is the acceleration due to gravity. This can be calculated using the equation: S = \dfrac One key aspect of projectile motion is the range of flight, which is the horizontal distance a projectile will travel before it hits the ground. These equations allow us to determine the position, velocity and acceleration of a projectile at any point in its flight. To calculate projectile motion, we use the equations of motion, which are derived from Newton's laws of motion. Examples of projectiles include balls being thrown or kicked, bullets being fired from a gun, and objects being launched from a catapult. Projectile motion is the motion of an object projected into the air, and then subject to only the force of gravity. What projectile motion is and how it can be calculated #Raised projectile motion calculator professional
Whether you are working on a school project or a professional engineering design, our calculator is an essential tool for anyone studying or working with projectiles.
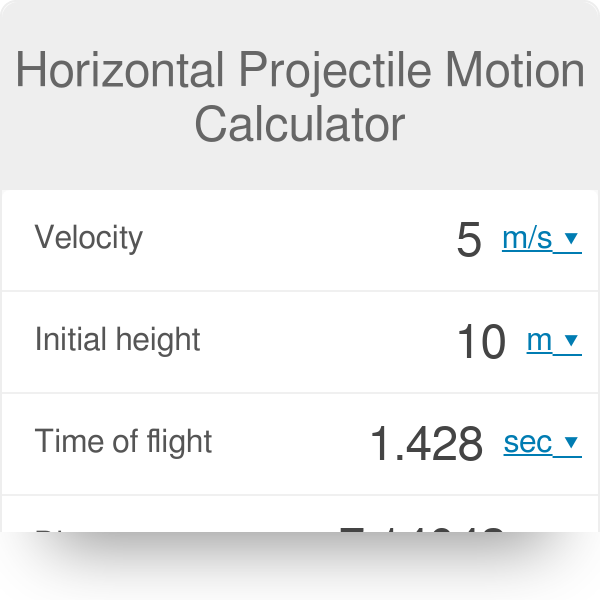
Simply select what to calc and input the required values into the calculator, and the results will be displayed instantly.īy using our projectile motion calculator, you can save time and ensure accuracy in your calculations.

If you are looking for a projectile motion calculator, you're in luck! Our projectile motion calculator can quickly and accurately calculate the range of flight, flight time, and maximum height of your projectile.








 0 kommentar(er)
0 kommentar(er)
